1．經歷數學建模的基本過程，能分析實際問題中變量之間的二次函數關系。

2．會運用二次函數求實際問題中的最大值或最小值。

3．能應用二次函數的性質解決商品銷售過程中的最大利潤問題。

一、情境導入

紅光旅社有100張床位，每床每日收費10元，客床可全部租出，若每床每日收費提高2元，則租出床位減少10張，若每床每日收費再提高2元，則租出床位再減少10張，以每提高2元的這種方式變化下去，每床每日應提高多少元，才能使旅社獲得最大利潤？

二、合作探究

探究點一：最大利潤問題

【類型一】利用解析式確定獲利最大的條件

為了推進知識和技術創新、節能降耗，使我國的經濟能夠保持可持續發展．某工廠經過技術攻關后，產品質量不斷提高，該產品按質量分為10個檔次，生產第一檔次(即最低檔)的新產品一天生產76件，每件利潤10元，每提高一個檔次，每件可節約能源消耗2元，但一天產量減少4件．生產該產品的檔次越高，每件產品節約的能源就越多，是否獲得的利潤就越大？請你為該工廠的生產提出建議．

解析：在這個工業生產的實際問題中，隨著生產產品檔次的變化，所獲利潤也在不斷的變化，于是可建立函數模型；找出題中的數量關系：一天的總利潤＝一天生產的產品件數×每件產品的利潤；其中，“每件可節約能源消耗2元”的意思是利潤增加2元；利用二次函數確定最大利潤，再據此提出自己認為合理的建議．

解：設該廠生產第x檔的產品一天的總利潤為y元，則有y＝[10＋2(x－1)][76－4(x－1)]＝－8x²＋128x＋640＝－8(x－8)²＋1152.當x＝8時，y_最大值＝1152.由此可見，并不是生產該產品的檔次越高，獲得的利潤就越大．建議：若想獲得最大利潤，應生產第8檔次的產品．(其他建議，只要合理即可)

【類型二】利用圖象解析式確定最大利潤

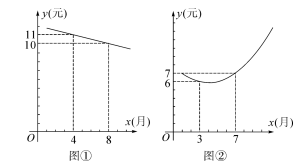
某水果店銷售某種水果，由歷年市場行情可知，從第1月至第12月，這種水果每千克售價y₁(元)與銷售時間第x月之間存在如圖①所示(一條線段)的變化趨勢，每千克成本y₂(元)與銷售時間第x月滿足函數關系式y₂＝mx²－8mx＋n，其變化趨勢如圖②所示．

(1)求y₂的解析式；

(2)第幾月銷售這種水果，每千克所獲得利潤最大？最大利潤是多少？

解：(1)由題意可得，函數y₂的圖象經過兩點(3，6)，(7，7)

∴

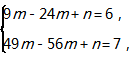
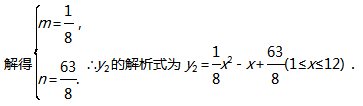
(2)設y₁＝kx＋b，∵函數y₁的圖象過兩點(4，11)，(8，10)

∴8k＋b＝10，4k＋b＝11，解得

∴y₁的解析式為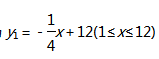

設這種水果每千克所獲得的利潤為w元．

則w＝y₁－y₂＝

∴w＝

∴當x＝3時，w取最大值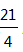

∴第3月銷售這種水果，每千克所獲的利潤最大，最大利潤是